Archivo mensual: julio 2010

Tarea Olímpica: Viernes 16 de julio

Escrito por magister en tarea olimpiada y etiquetada con ,
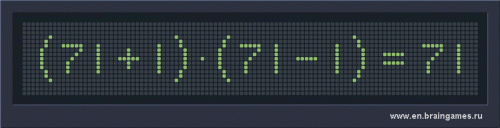
  • Una araña tiene 8 calcetines y 8 zapatos, numerados para cada una de sus patas. ¿En cuantos órdenes distintos puede ponerse los calcetines y los zapatos si no puede ponerse el zapato correspondiente una pierna sin antes ponerse el calcetín de la misma?
  • Un cajón tiene 100 calcetines rojos, 80 verdes, 60 azules y 40 negros. Si saca calcetines de uno en uno sin mirar, ¿cuantos tiene que sacar para asegurarse de tener 10 pares? (cada par está formado por dos calcetines de un mismo color, cualquiera que sea éste).
  • ¿De cuantas formas puedes escoger 5 elementos del conjunto {1,2,3,…,18} de forma que cualquiera dos de los escogidos tengan una diferencia de al menos 2?
  • Demuestra que si n es impar,  entonces la lista
    \binom{n}{1},\binom{n}{2},\binom{n}{3},\ldots,\binom{n}{\frac{n-1}{2}}
    contiene una cantidad impar de términos impares.
  • Prueba que si escoges 16 enteros distintos del conjunto {1,2,3,…100}, existen cuatro de ellos a, b, c, d tales que a+b=c+d.  Determina si esta cota es la mínima posible.
  • Manuel ha escogido 4 números del conjunto {1,2,3,4,5,6,7}. Si Manuel le dice a Dulce el producto de los 4 números, esta información no es suficiente para que Dulce pueda saber qué números son. ¿Cuanto vale el producto de los 4 números?
  • Sea k un número par. Demuestra que no es posible encontrar números positivos a_1, a_2,\ldots,a_k impares tales que 1=\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_k}.
  • Si n es un entero positivo, demuestra que 3^{2^n}+1 es par pero no divisible por 4.

Los primeros 5 problemas aparecen en el libro 102 Combinatorial Problems from the Training of the USA IMO Team, los demás en 104 Number Theory Problems, ambos de Titu Andreescu

Diagramas de Young

Escrito por magister en ilustración y etiquetada con ,
Media_httpuploadwikim_wqpgo
Imagen de Wikimedia Commons (R.A. Nonenmacher)
Diagramas de Young de las particiones hasta con 8 partes

Acertijo

Escrito por magister en problema y etiquetada con ,

 

Tumblr_l5678evgyk1qcc3y1o1_1280

 

La expresión es cierta, pero hay un pixel defectuoso. ¿Cual es?

Minucias del lenguaje

Escrito por magister en random y etiquetada con

http://www.fondodeculturaeconomica.com/obras/suma/r3/buscar.asp

Artículos sobre particularidades del idioma español, especialmente del hablado en México

Examen final: Matemáticas discretas I, 2010

Escrito por magister en combinatoria, univ y etiquetada con , , , ,

El examen se aplicó a los estudiantes de la licenciatura de Física-Matemáticas en dos fechas, el 30 de junio (la fecha programada) y otra opción el 6 de julio para quienes querían esperar algunos días.

Examen del 30 de junio.

INSTRUCCIONES: Selecciona 5 de los 6 problemas y resuélvelos.

Problema 1. Demuestra que el número de soluciones enteras y positivas de la ecuación x_1+x_2+x_3+x_4=9 es el mismo que el número de soluciones enteras y positivas de la ecuación x_1+x_2+x_3+x_4+x_5+x_6=9.

Problema 2. Las fichas en un juego de poker pueden ser rojas, azules o blancas. ¿De cuántas formas se puede hacer un montón con 12 fichas?

Problema 3. Demuestra mediante alguna biyección que si X es un conjunto con n elementos, entonces la
cantidad de subconjuntos con un número par de elementos es la misma que la cantidad de subconjuntos con un número impar de elementos.

Problema 4. Sea G una gráfica simple con 10 vértices y 28 aristas. Demuestra que contiene un ciclo de
longitud 4.

Problema 5. Demuestra usando un argumento combinatorio que
\binom{n}{1} + 2\binom{n}{2} + 3\binom{n}{3} + \cdots + n\binom{n}{n}= n 2^{n-1}.

Problema 6. Encuentra dos gráficas simples y conexas que tengan la misma sucesión de grados pero que no sean isomorfas (¡demuestra que no lo son!).

Examen del 6 de julio.

INSTRUCCIONES: Selecciona 5 de los 7 problemas y resuélvelos.

Problema 1. ¿De cuántas formas puedes acomodar en fila 10 unos y 5 ceros de tal forma que no haya dos ceros en posiciones contiguas?

Problema 2. ¿Cuántas gráficas simples con 12 vértices existen?

Problema 3. ¿Cuántas soluciones tiene la ecuación x_1+x_2+x_3+x_4+x_5=24 si cada x_i es entera y positiva?

Problema 4. Si m⩾n⩾2,
a) ¿Cuántos ciclos de longitud 4 hay en la gráfica K_{m,n}?
b) ¿Cuántas trayectorias de longitud 2 hay en K_{m,n}?
c) ¿Cuántas trayectorias de longitud 3 hay en K_{m,n}?

Problema 5. Demuestra usando un argumento combinatorio que (n-k)\binom{n}{k} = n\binom{n-1}{k}.

Problema 6. Si d_n es el número de formas de cubrir una cuadrícula de 2×n con dominós, demuestra que
d_{n+2}=d_0 + d_1 + d_2 + \cdots + d_{n-1}+d_n .

Problema 7. Sea X = {1,2,3,…,20}. Demuestra mediante alguna biyección que la cantidad de subconjuntos de
X con un número par de elementos es la misma que la cantidad de subconjuntos de X con un número impar de elementos.